今天阿莫来给大家分享一些关于关于tan诱导公式的信息tan诱导公式是什么 方面的知识吧,希望大家会喜欢哦
1、tan诱导公式如下:tan正切函数的诱导公式是tan(π+α)=tanα,tan(-α)=-tanαtan(π-α)=-tanα,tan(2π+α)=tanα,tan(2π-α)=-tanα,tan(π-α)=-tanα。
2、tan的诱导公式是tanα±tanβ=sin(α±β)/(cosα·cosβ),在Rt△ABC(直角三角形)中,∠C=90°,AB是∠C的对边c,BC是∠A的对边a,AC是∠B的对边b,正切函数就是tanB=b/a,即tanB=AC/BC。
3、cot诱导公式cot(kπ+α)=cotαcot(π/2-α)=tanαcot(π/2+α)=-tanαcot(-α)=-cotαcot(π+α)=cotαcot(π-α)=-cotα三角函数三角函数是数学中属于初等函数中的超越函数的一类函数。
4、正切函数诱导公式是tan(2π+α)=tanα,诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。
5、tan2a=2tana/[1-tan2(a)]。三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。
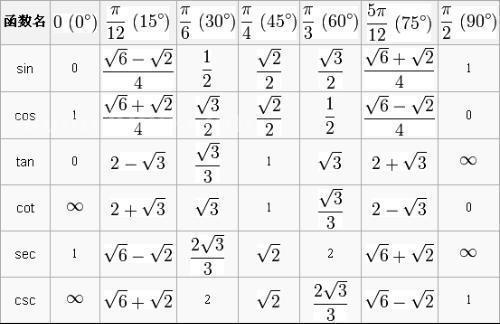
1、tan诱导公式如下:tan正切函数的诱导公式是tan(π+α)=tanα,tan(-α)=-tanαtan(π-α)=-tanα,tan(2π+α)=tanα,tan(2π-α)=-tanα,tan(π-α)=-tanα。
2、tan的诱导公式是tanα±tanβ=sin(α±β)/(cosα·cosβ),在Rt△ABC(直角三角形)中,∠C=90°,AB是∠C的对边c,BC是∠A的对边a,AC是∠B的对边b,正切函数就是tanB=b/a,即tanB=AC/BC。
3、tan(π/2+α)=-cotα,tan(π/2-α)=cotα。诱导公式是指三角函数中,利用周期性将诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。诱导公式有六组,共54个。
4、正切函数诱导公式是tan(2π+α)=tanα,诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。
5、诱导公式推导是:*公式推导:sin2α=2sinαcosα=2sinαcosα/[cos2(α)+sin2(α)],(因为cos2(α)+sin2(α)=1)。再把分式上下同除cos^2(α),可得sin2α=2tanα/[1+tan2(α)]。
tan的诱导公式是tanα±tanβ=sin(α±β)/(cosα·cosβ),在Rt△ABC(直角三角形)中,∠C=90°,AB是∠C的对边c,BC是∠A的对边a,AC是∠B的对边b,正切函数就是tanB=b/a,即tanB=AC/BC。
正切函数诱导公式是tan(2π+α)=tanα,诱导公式是指三角函数中,利用周期性将角度比较大的三角函数,转换为角度比较小的三角函数的公式。
cot和tan的关系:tanα·cotα=1。在三角函数中,cotθ=cosθ/sinθ,当θ≠kπ,k∈Z时,cotθ=1/tanθ,当θ=kπ,k∈Z时,cotθ不存在。
1、正切函数的诱导公式是tan(π+α)=tanα;tan(-α)=-tanαtan(π-α)=-tanα。正切函数一般指正切。
2、正切函数公式tanA=a/b。三角函数是数学中属于初等函数中的超越函数的函数。它们的本质是任何角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的。
3、先利用单位圆(向量)推到两角和与差的余弦公式,再利用诱导公式推导正弦公式,最后利用同角三角函数的基本关系推到正切公式。
4、三角函数诱导公式口诀:一全正、二正弦、三正切、四余弦;全,S,T,C,正;奇变偶不变、符号看象限;正弦一二切一三,余弦一四紧相连,言之为正。
5、这些角度的三角函数值是经常用到的。并且利用两角和与差的三角函数公式,可以求出一些其他角度的三角函数值。常见的三角函数包括正弦函数、余弦函数和正切函数。
6、三角函数诱导公式:所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。下面就和我一起了解一下吧,供大家参考。
本文到这结束,希望上面文章对大家有所帮助